Hertsi, sentti ja desibeli
Mainittuja käsitteitä voidaan pitää jonkinlaisina perusmittayksikköinä musiikkiakustiikassa.
Hz (hertsi)
Hertsi (Hz) on värähtelytaajuuden mittayksikkö aaltoliikkeessä. Taajuus on 1 Hz kun tapahtuu yksi värähdys sekunnissa. Kun sekuntia kohden on 1 000 värähdystä, taajuus on 1 000 Hz eli 1 kHz.
Sävelten nimet lähtevät subkontraoktaavin C:stä (C2). Sen taajuus on n. 16 Hz (värähdystä sekunnissa). Tätä taajuutta on lähes mahdotonta aistia sellaisenaan. Soittimissa (esim. urut) siihen liittyykin erinäinen määrä osaääneksiä, jotka mahdollistavat sävelkorkeuden aistimisen.
Kun taajuus on useita tuhansia hertsejä ääni voidaan kuulla, mutta sen sävelkorkeuden määrittely muuttuu hankalaksi. Yleensä sävelkorkeuksien määrittely loppuu "kuusiviivaiseen c:hen (c6), jonka taajuus on 8 370 Hz.Tätä korkeammille sävelille on vaikea hahmottaa sävelkorkeutta.
Taajuuksia (frekvenssejä) voidaan aistia aina n. 20 kilohertsiin (20 kHz) saakka, kuten jo aiemmin tuli mainittua. Raja on kuitenkin hyvin summittainen ja riippuu monista tekijöistä, mm. äänen intensiteetistä. Jotkut nuoret henkilöt pystyvät aistimaan tätä korkeammatkin äänet muutenkin kuin paineen muutoksena korvan sisällä. Iän myötä kuuloaistimuksen yläraja kuitenkin väistämättä alenee ja monilla iäkkäillä henkilöillä on vaikeuksia kuulla jopa alle 10 kHz:n taajuuksia vaikka ne olisivat voimakkaitakin.
Kuuloalueen määrittely esim. arvoiksi 16 Hz - 20 kHz on siis hyvin keinotekoista ja jonkinlainen keskiarvo, joka koskee vain nuorta väestöä.
Taajuuden  , aallonpituuden
, aallonpituuden  ja äänen
nopeuden
ja äänen
nopeuden  välillä ovat
yhtälöt:
välillä ovat
yhtälöt:
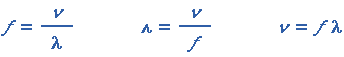
Jos siis äänen taajuus on esim. 440 Hz (eli sävel a1) ja äänen nopeus n. 330 m/s, saadaan aallonpituudeksi 330/440 metriä eli 75 cm. Näin etäällä toisistaan ovat siis ääniaallon peräkkäiset tihentymät.
Äänen nopeus riippuu sekä väliaineesta (metalli, vesi, ilma) että lämpötilasta. Ilmassa äänen nopeus on 331,4 m/s kun lämpötila on 0°C, mutta lisääntyy 0,6 m/s jokaista astetta kohden kun lämpötila nousee. Huonelämpötilassa (22°C) äänen nopeus on n. 345 m/s. Seuraavaksi voit itse kokeilla miten äänennopeus muuttuu suhteessa ilman lämpötilaan:
Mikä on äänen nopeus suomalaisessa saunassa (+80o)?
Mikä on äänen nopeus talvipakkasella (-30o)?
Yli 20 kHz:n taajuuksia kutsutaan ultraääniksi ja alle 16 Hz:n taajuuksia vastaavasti infraääniksi. Nimitys hertsi johtuu saksalaisesta fyysikosta Rudolf Herzistä (1857-94), joka ensimmäisenä kokeellisesti osoitti radioaaltojen leviämisen.
C (sentti, engl. cent < lat. centum = sata)
Yleisin mikrointervallien mittaamiseen käytetty yksikkö on nimeltään sentti (C, engl. cent, saks. Cent < lat. centum = sata). Se tarkoittaa tasavireisen puoliaskelen sadasosaa, eli oktaavi on 1 200 senttiä.
Tasavireinen kokoaskel voidaan ilmaista symbolilla 200 C ja tasavireinen kvintti on 700 C eli seitsemän puoliaskelta.
Yksikköä sentti käytetään sekä mikrointervallin koon ilmaisemiseen että minkä tahansa intervallin (sekunti, terssi jne.) suhdeluvun havainnollistamiseen. Eri viritysjärjestelmissä käytettyjen intervallien eroja voidaan vertailla senttiarvojen avulla, tasavireisyydessä ne ovat aina satalukuja.
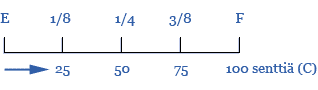
Alla olevassa kuviossa on vertailtu tyypillisiä mikrointervallien murtolukuesityksiä ja vastaavia senttiarvoja sävelten e ja f välillä. Neljäsosasävelaskel on siis 50 C ja kahdeksasosasävelaskel 25 C.
Murtolukujen avulla on perinteisesti esitetty myös intervallien suhdelukuja. Murtolukujen käyttö on ollut luontevaa, koska mm. pythagoralainen ja puhdas viritys(järjestelmä) perustuvat niiden käyttöön. Niiden keskinäinen vertailu on kuitenkin usein hankalampaa kuin vastaavien desimaaliarvojen. On esimerkiksi hankala arvioida, että 16/9 on arvoltaan suurempi kuin 7/4 (desimaaleina 1,78 > 1,75).
Intervallierotuksia kuvaavat murtoluvut voidaan esittää senttiarvoina seuraavan muuntokaavan avulla:
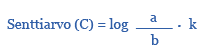
Symbolit a ja b ovat murtoluvun osia ja k on vakio 1 200/10log 2 = 3986,313715...
Esim. luonnonpuhdas kvintti esitetään yleensä suhdelukuna 3/2,
jonka logaritmi on n. 0,176.
Tämä kerrottuna k:lla on n. 702. Toisin sanoen puhdas kvintti on
tasavireistä kvinttiä noin kaksi senttiä laajempi intervalli.
Esimerkiksi pienen a:n sävelkorkeus on 220 Hz. Yksiviivainen e on näin
ollen n. 330 Hz (= 3/2 · 220). Yksiviivainen a on 440 Hz ja kaksiviivainen
e noin 660 Hz ( = 3/2 · 440). Sama intervalli kuuloalueen ala- ja yläpäässä on
hertsisuhteiltaan hyvin erilainen. Esim. oktaavi on sekä alue 40....80
Hz että alue 4000....8000 Hz. Sama intervalli voidaan ilmaista suhdelukuna
kahdella eri tavalla; suurempi luvuista on aina "se korkeampi sävel".
Kun esim. kvinttisuhde esitetään 3/2:n sijasta 2/3, niin senttiarvosta
tulee negatiivinen ("kvintti alaspäin") (-702).
Senttiarvo voidaan muuttaa desimaaliarvoksi jakamalla se ensin vakio k:lla ja sijoittamalla saatu arvo luvun 10 eksponentiksi. Esim. 702 C/k = 0,176 ja 10 0,176 = 1,5 eli 3/2.
Hertsiarvoja voi muuttaa senteiksi ja päinvastoin helposti myös syöttämällä alla olevaan "laskimeen" erilaisia arvoja. Käytä pilkun sijasta pistettä, jos syöttämäsi luvut sisältävät desimaaleja.
|
dB (desibeli)
Desibeli on äänenvoimakkuuden suhteellinen mittayksikkö. Hiljaisin normaalilla (keskimääräisellä) kuuloaistilla havaittava ääni on desibeleinä 0 dB (äänipainearvona 2 · 10-5 Pascalia ja intensiteettiarvona ilmaistuna 10-12 W/m2, jos taajuus on 1 000 Hz). Hyväkuuloinen kuulee jopa tätä heikompia ääniä (- 5dB). Kun äänen intensiteetti (pinta-alan läpi virtaava energia) kaksinkertaistuu, niin desibelit lisääntyvät 3:lla. Äänipaineen kaksinkertaistuessa intensiteetti nelinkertaistuu, jolloin lisäys on jo 6 dB. Satakertainen äänentehon vahvistus vastaa äänipainetason kymmenkertaistumista, mutta desibeleissä mitattuna lisäys on vain 20 dB. Desibeliasteikko on siis logaritminen.
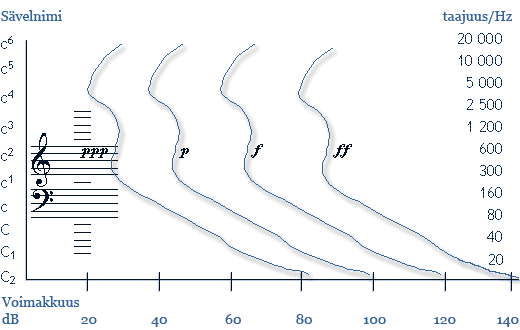
Aistittu äänen voimakkuus riippuu äänipainetasosta ja äänen korkeudesta. Tietyt taajuudet kuullaan herkemmin kuin toiset. Joskus koetusta äänenvoimakkuudesta käytetään termiä kuuluvuus. Alla olevassa kuviossa on esitetty vasemmalla kuuloalue nuottikuvana ja sävelniminä, oikealla taas hertseinä. Kaaviosta havaitaan, että korvan herkin alue sijoittuu suurin piirtein neliviivaisen oktaavin alueelle. Äänipainetasoa mitataan nykyisin ns. painotetulla desibeliasteikolla (esim. dBA), jossa otetaan huomioon se, että ihmiskorva ei ole mittalaite vaan kuulee eri tavoin eri sävelkorkeuksia.
Käsitteitä foni (phon) ja soni (sone) on käytetty mitattaessa kuuloaistimuksen voimakkuutta. Ensin mainitussa kuultua ääntä verrataan 1 000 Hz taajuuteen. Kun äänet tuntuvat yhtä voimakkailta ne saavat saman arvon, vaikka äänipainetasot eroaisivatkin huomattavasti toisistaan. Soniarvo määräytyy myös vertailun tuloksena: kun ääni kuulostaa toistettuna kaksi kertaa niin voimakkaalta kuin alunperin kuultu, se saa kaksinkertaisen soniarvon. Yksiköt ovat subjektiivisia ja vaikeasti mitattavia.
Kuvion 'piano'- ja 'forte'-käyrätkin ovat hyvin summittaisia. Niistä voidaan kuitenkin havaita, esim. että matala C1 (32 Hz) aistitaan ppp:na vaikka saman desibelitasoinen (60 dB) c5 (n. 4 200 Hz) aistitaankin fortena.