Doppler-ilmiö
Doppler-ilmiöllä tarkoitetaan äänen taajuudessa havaittavaa muutosta, joka johtuu havaitsijan ja äänilähteen liikkeestä toistensa suhteen. Kun ne lähestyvät toisiaan äänen sävelkorkeus nousee, koska aallot ikäänkuin tihenevät. Etäännyttäessä sävelkorkeus taas laskee aaltoliikkeen harventuessa. Doppler-ilmiötä voidaan havainnollistaa myös visuaalisesti.
Äänilähteenä voi toimia esim. auto sen kulkiessa moottoritiellä. Auton ohittaessa sen aikaansaaman äänen sävelkorkeus laskee. Auton vauhdin voi päätellä intervallista alla olevan taulukon mukaan. Jos ohitustilanteessa kuultava laskeva intervalli on suuri terssi, niin auto ajaa ylinopeutta (yli 120 km/h).
| suhdeluku | kulkuneuvon nopeus | erotus oktaavin 1200-osina eli sentteinä |
intervalli |
| s | (1-2)*1220/(s+1) | 3986*log s | |
| 0,71 | 207 | 593 | tritonus |
| 0,72 | 199 | 569 | |
| 0,73 | 190 | 545 | |
| 0,74 | 182 | 521 | |
| 0,75 | 174 | 498 | kvartti |
| 0,76 | 166 | 485 | |
| 0,77 | 159 | 452 | |
| 0,78 | 151 | 430 | |
| 0,79 | 143 | 408 | suuri terssi |
| 0.80 | 136 | 386 | luonn. duuriterssi |
| 0.81 | 128 | 365 | |
| 0.82 | 121 | 344 | |
| 0.83 | 113 | 323 | |
| 0.84 | 106 | 302 | pieni terssi |
| 0.85 | 99 | 281 | |
| 0.86 | 92 | 261 | |
| 0.87 | 85 | 241 | |
| 0.88 | 78 | 221 | |
| 0.89 | 71 | 202 | suuri sekunti |
Kaava Doppler-ilmiön laskemiseksi:
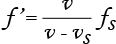 |
 |
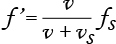 |
| kohteen lähestyessä | kohteen etääntyessä |
Esimerkiksi auton äänitorvi on 440 Hz. Mikä on taajuus
a) auton lähestyessä 90 km/h eli 25 m/s) —> 475
Hz
b) auton etääntyessä 90 km/h —> 410 Hz
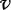 = 343
= 343
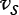 = 25
= 25
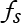 = 440
= 440
Auton ohittaessa kyseisten hertsilukujen erotus on se, mitä korva kuulee. Tässä tapauksessa erotus on kokoaskeleen ja pienen terssin välillä (255 senttiä).
Edellä olevan taulukon avulla saadaan suoraan suhdeluku 410/475 = 0, 863... -> n. 250 –260 C
Myös lämpötila vaikuttaa hiukan äänenkorkeuden muutokseen doppler-ilmiössä:
| 0° C | 13° C | 20° C | |
| äänen nopeus km/h | 1191 | 1220 | 1235 |
| ajoneuvon nopeus, jotta inetrvalli pysyisi samana | 96,6 | 98,9 | 100,1 |

